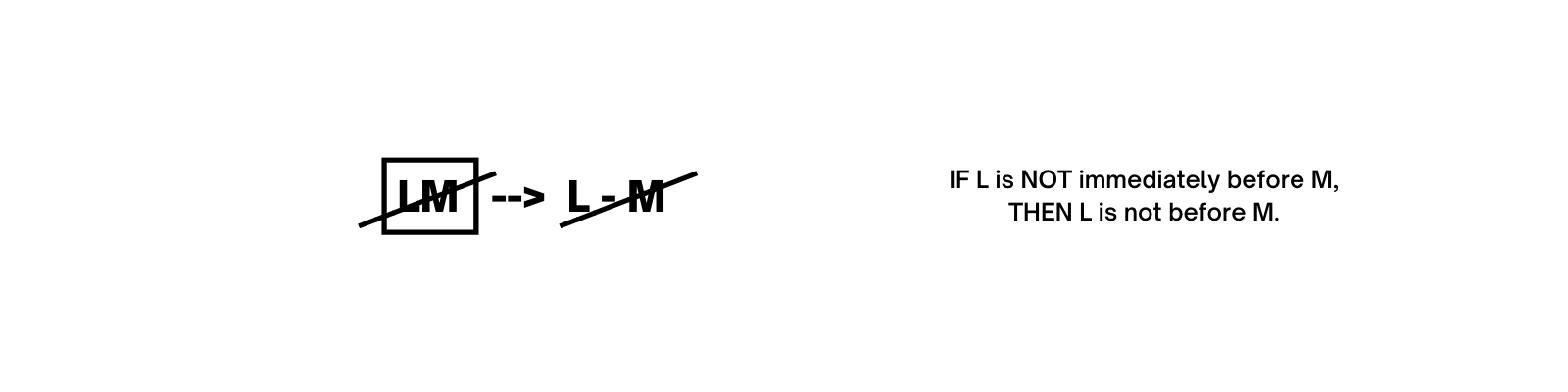This post is part three in a series on how to diagram linear game rules. The goal is to give you “plain English” explanations of challenging LG rules so that you can diagram them with confidence.
The rules
Part 1
- Usain finished the race 3 spots in front of Carl.
- Usain finished the race at least 3 spots in front of Carl.
- Usain finishes before Carl, and at least one other person finishes between them.
Part 2
- Turner is before Quinn or after Fernandez but not both.
- Neither Fernandez nor Quinn can be seen before Turner.
- Fernandez and Quinn cannot both be seen before Turner.
- Either Fernandez or Quinn, but not both, must be seen before Turner.
Part 3
- If Samuel is before Jacqueline, then Marco must be after Liu.
- Samuel is before Jacqueline only if Marco is after Liu.
- If Liu is before Marco, he must be immediately before Marco.
- Samuel must be immediately after Jacqueline unless Liu is before Marco.
Conditional Reasoning
This post assumes that you’ve had an introduction to how to diagram formal logic and how to form the contrapositive. If not, you might want to get that background and then come back. Khan Academy has a good introduction in the Logic Toolbox section of their free online LSAT course.
But here’s a quick note about the contrapositive, since it can be tricky for students. Remember that the contrapositive of a formal logic statement is another statement that is logically equivalent and therefore also true. In plain English, it’s something else that we know to be true.
Consider this sentence: “If I miss the train, I’ll be late to work.” What we also know is that if you weren’t late to work, you must not have missed the train. That’s the contrapositive.
Miss the train → Late to work
Not late to work → Didn’t miss the train
A word of caution
Be careful about what triggers what. It’s tempting to read these backward sometimes.
What if I was late to work? Do you KNOW that’s because I missed the train? Not really. Maybe I caught the train, but then decided to get coffee after exiting the train, and that’s what made me late to work. Or maybe I was late because I just didn’t feel like showing up on time. It’s not right to assume that Late to work → Miss the train.
Same thing with reading the contrapositive backward. Let’s say I didn’t miss the train. Does that mean I wasn’t late to work? Not really. For the same reasons. Maybe I stopped for coffee. Maybe I just don’t like my job and didn’t show up on time. We can’t assume that Didn’t miss the train → Not late to work.
Rule 3a: If Samuel is before Jacqueline, then Marco must be after Liu.
We’re starting out here with a relatively straightforward conditional rule. We’ll build on it as we get further into this post.
We first want to separate the conditional statement into the sufficient (if) part and the necessary (then) part. In plain English, we want to identify what part of the sentence will trigger which other part of the sentence. Or which part, if it happens, will guarantee that the other part of the sentence also happens.
Sufficient: Samuel is before Jacqueline. S – J
Necessary: Marco is after Liu. L – M
In other words, anytime we see Samuel before Jacqueline, we’ll also need to have Marco after Liu.
We can diagram the rule like this, using an arrow to represent that the first half will trigger the second half:
The contrapositive
The steps to forming the contrapositive is to swap the sufficient and necessary conditions (swap the if and the then parts of the sentence) and negate them.
We can also think about this in plain English too. It just might require you to really think about it for a bit. (If it gives you a headache right now, keep thinking about it. Come back to it. Eventually it will click. It just takes time.)
We know that if Samuel is before Jacqueline, then Marco has to be after Liu. But what if Marco ISN’T after Liu? What if he’s BEFORE Liu? Well, then Samuel must not have been before Jacqueline, because if he had been before her, then Marco would have to be after Liu. This situation of Marco not being after Liu is our contrapositive.
Contrapositive Sufficient: Marco is not after Liu.
Contrapositive Necessary: Samuel is not before Jacqueline.
Some students stop there because they’ve been trained to form the contrapositive by swapping the order and negating the elements. But we can do better.
Think about what it means for Marco to not be after Liu. Assuming no funny business like they can be at the same time, this means that Marco is before Liu. And Samuel being not before Jacqueline means that he’s after her.
So we really get this:
Contrapositive Sufficient: Marco is before Liu. M – L
Contrapositive Necessary: Samuel is after Jacqueline. J – S
We can diagram it this way:
Rule 3b: Samuel is before Jacqueline only if Marco is after Liu.
The formal logic phrase here is “only if.” This one can be a tricky one for students because the “if” in it is misleading.
How to treat “only if”
Think about this sentence “I’ll buy you dinner only if it’s your birthday.” And ask yourself whether it really truly means “If it’s your birthday, I’ll definitely buy you dinner.” It actually doesn’t. It means “I’ll buy you dinner only if it’s your birthday. There’s no other situation in which I would buy you dinner. So if you see me buying you dinner, you can know that it’s your birthday.”
This means the “only if” actually signals the necessary condition rather than the sufficient.
To deal with it, replace “only if” with a “then.” Then add an “if” to the other part of the sentence.
“If I buy you dinner, then it’s your birthday.”
Translating “only if”
For Samuel and friends, that means “Samuel is before Jacqueline only if Marco is after Liu” should be treated as “If Samuel is before Jacqueline, then Marco is after Liu.”
Sufficient: Samuel is before Jacqueline. S – J
Necessary: Marco is after Liu. L – M
That’s exactly what we had in Rule 3a, so we’ll diagram it and the contrapositive the same as before:
Rule 3c: If Liu is before Marco, he must be immediately before Marco.
We’ve got a twist here with the “immediately before.” But it’s nothing we can’t handle.
We’ve been signally “before” and “after” with dashes. So we just need a different way to indicate that something is right before, not just somewhere before. You’ll see many prep books doing that by just not using the dash. Just shove those two letters together. Some prep books emphasize the relationship a little more by putting the two letters in a box together to show that no one can get in between them.
So let’s do that, first by starting out listing the sufficient and necessary conditions.
Sufficient: Liu is before Marco. L – M
Necessary: Liu is immediately before Marco. LM
Or:
The contrapositive
We’ll follow the same steps as before, swapping the sufficient and necessary conditions and negating them.
Contrapositive Sufficient: Liu is not immediately before Marco. not LM
Contrapositive Necessary: Liu is not before Marco. not L – M
Or:
But we can simplify the necessary condition a little. We know that Liu not being before Marco means he has to be after Marco. So we really get this:
Contrapositive Sufficient: Liu is not immediately before Marco. not LM
Contrapositive Necessary: Liu is after Marco. M – L
Or:
Advanced mode: Getting to the heart of the rules
Let’s return to the original rule 3c: If Liu is before Marco, he must be immediately before Marco. We diagrammed that as the following:
But we can do better. Let’s think about what it really means by thinking about OK and Not OK scenarios (the technique we used in Part 2).
Not OK
- Liu is somewhere before Marco, but there’s someone else between them. ← This would violate the conditional rule. If Liu is somewhere before Marco, he’s supposed to be immediately before.
OK
- Liu is immediately before Marco. ← This happens when the rule gets triggered. We’ve got Liu before Marco, so he’s immediately before Marco.
Also OK
- Liu is after Marco. ← This is the possibility students often don’t see. It comes from not triggering the rule in the first place.
Consider the sentence “If it rains, I’ll be in the library.” What happens if it’s not raining? You don’t know! Maybe I’ll be in the park, maybe I’ll be at home, but maybe I’ll be in the library anyway. When the “if” part of the sentence isn’t triggered, anything can happen.
So our two possibilities here are that the rule gets triggered (putting Liu right before Marco) or the rule doesn’t get triggered (because Liu is after Marco).
We could diagram it like this:
The cool part is that this way of diagramming actually means we don’t need the contrapositive either. These two possibilities cover the contrapositive as well.
This reinterpretation won’t always work though. It only works here because both halves of the conditional were about Liu and Marco. It didn’t work in Rule 3a or Rule 3b because we also had Samuel and Jacqueline involved so there wasn’t any overlap between the sufficient and necessary conditions.
Rule 3d: Samuel must be immediately after Jacqueline unless Liu is before Marco.
“Unless” can cause major problems for students. It’s honestly the most confusing formal logic word for most students.
How to treat “unless”
The trick is to treat an “unless” like an “if not.”
So we can reread this rule as “if Liu is not before Marco, then Samuel must be immediately after Jacqueline.”
Sufficient: Liu is not before Marco.
Necessary: Samuel is immediately after Jacqueline.
Just like before, we’ll translate Liu not being before Marco as Liu being after Marco. So we get this:
Sufficient: Liu is after Marco. M – L
Necessary: Samuel is immediately after Jacqueline. JS (in a box)
Or:
The contrapositive
Let’s do the same swapping and negating as before.
Contrapositive Sufficient: Samuel is not immediately after Jacqueline.
Contrapositive Necessary: Liu is not after Marco.
And then we’ll retranslate like before.
Contrapositive Sufficient: Samuel is not immediately after Jacqueline. JS in a box crossed out
Contrapositive Necessary: Liu is before Marco. L – M
Notice that we’re not going to retranslate Samuel not being immediately after Jacqueline. We could if we wanted. But that would mean we’d have to consider EITHER Samuel being before Jacqueline OR Samuel being somewhere later on after Jacqueline, just not immediately after her. That’s probably more confusing than just saying “don’t do JS.”
So here’s how we’d diagram the contrapositive:
Bonus Question
How would you diagram this?
Samuel must be immediately after Jacqueline unless he is before Jacqueline.
Send me a message to check your answer.
What’s next
Didn’t catch the either parts of this series? Go back and catch up.
Part 1
- Usain finished the race 3 spots in front of Carl.
- Usain finished the race at least 3 spots in front of Carl.
- Usain finishes before Carl, and at least one other person finishes between them.
Part 2
- Turner is before Quinn or after Fernandez but not both.
- Neither Fernandez nor Quinn can be seen before Turner.
- Fernandez and Quinn cannot both be seen before Turner.
- Either Fernandez or Quinn, but not both, must be seen before Turner.
LSAT Notes
If this post resonated with you, I’d love to stay in touch. About once a week, in the form of an email newsletter, I share useful strategies and insights I’ve picked up during my years teaching the LSAT. “LSAT Notes” you can use to study more effectively and raise your score.
Often these are inspired by breakthroughs my students had that week. Other times, they respond to questions students like you have. My goal is to provide motivation and encouragement along with knowledge about the test and advice about how to study.
Learn more about it here, or to subscribe, simply fill in the form below.